逻辑斯蒂回归

逻辑斯蒂回归是一个分类模型

分类问题

相比于回归，分类问题的结果是离散的值（或者类别的概率）

逻辑函数

$$
\sigma(x)=\frac{1}{1+e^{-x}}
$$

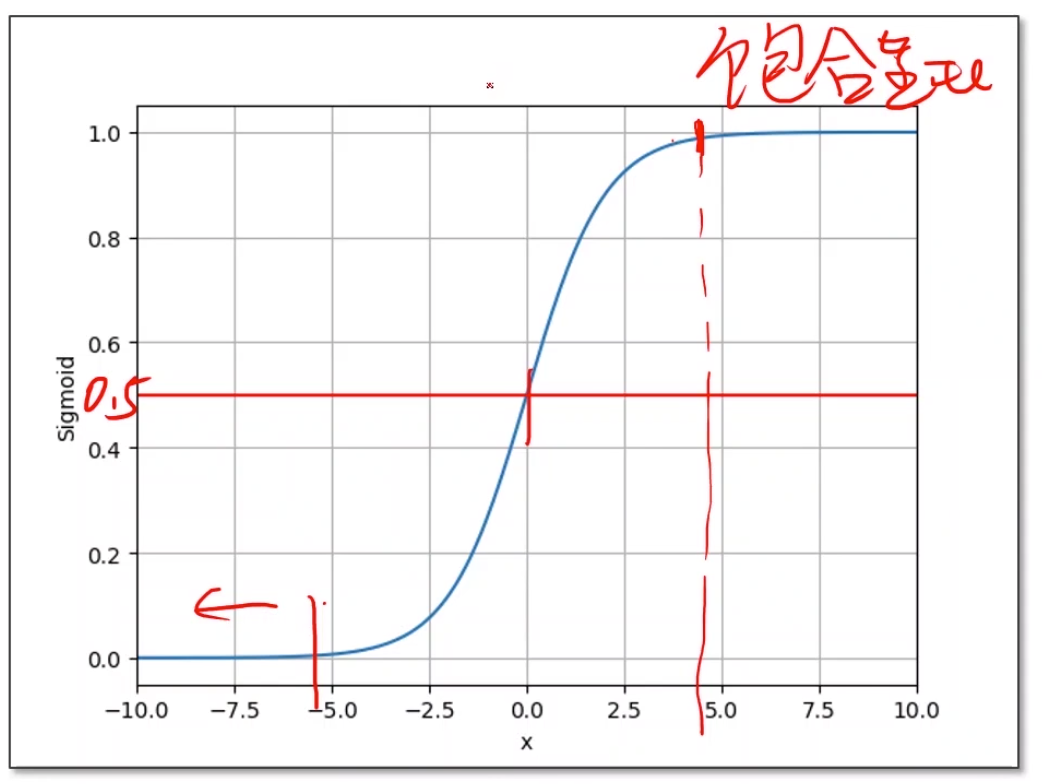
上面的逻辑函数是sigmoid函数（其实sigmoid是一类函数的叫法，特征是$[-1,1]$内单增的饱和函数，逻辑函数是其中最典型的一种），它是一个饱和函数（随着值的增大导数趋近于零），作用是把无穷区间上的值映射到$[0.0,1.0]$之间。最简单的做法，可以把线性模型$\hat{y} = x * \omega + b$的输出作为sigmoid的输入，以得到$[0.0,1.0]$之间的概率：

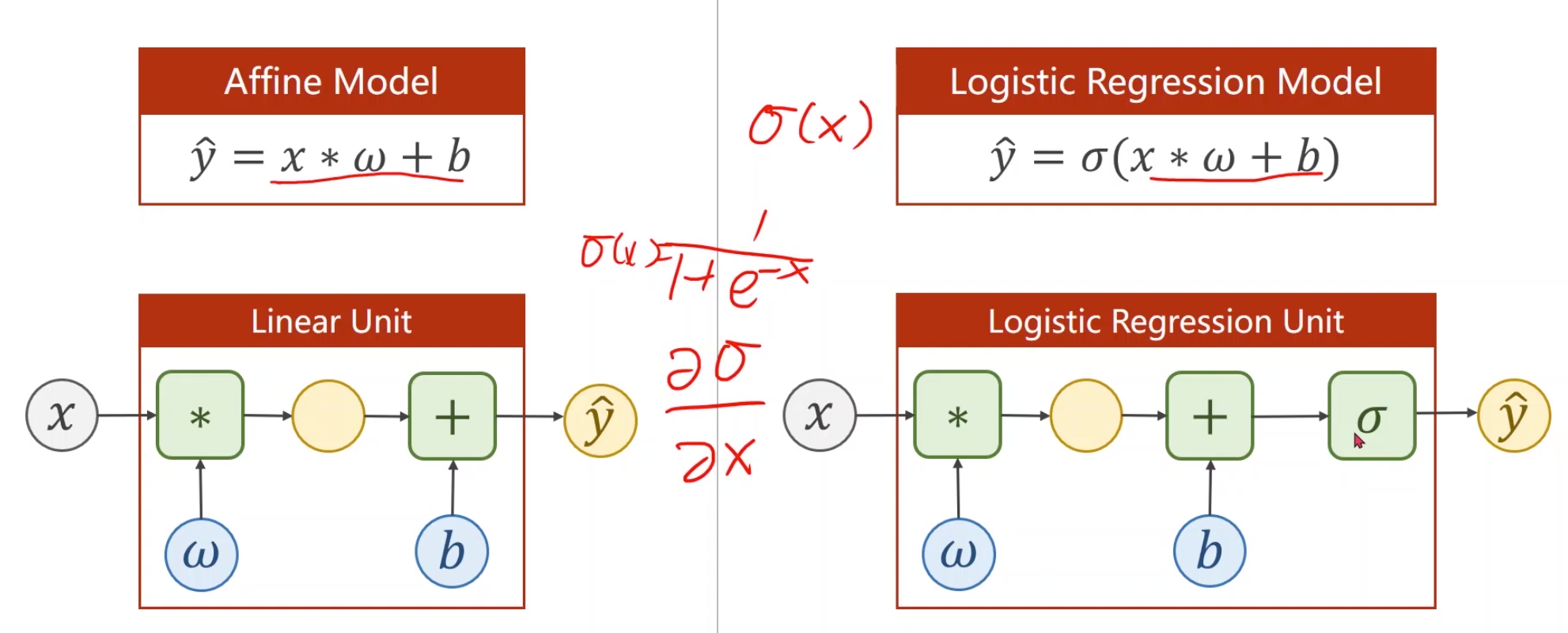
对应的损失函数也要发生变化：

上图中的第二个loss函数就是交叉熵：

假设有两个概率分布$P_D$和$P_T$，则衡量它们差异的交叉熵公式为：

$$
\sum_iP_D(X=i)\ln P_T(X=i)
$$

与一般的信息熵相比，主要差别在于事实的概率乘以预测的概率的ln

图中公式二（BCE, Binary Cross Entropy）优化的目标是loss最小，对应事实的分布与预测的分布最接近

二分类的交叉熵代码很简洁：

def CrossEntropy(yHat, y):
    if y == 1:
      return -log(yHat)
    else:
      return -log(1 - yHat)

针对多个样本的情况可以取一下均值：

或者网上有另一种形式更好理解些：

$-\sum_{c=1}^My_{o,c}\log(p_{o,c})$

M - number of classes (dog, cat, fish)
log - the natural log
y - binary indicator (0 or 1) if class label $c$ is the correct classification for observation $o$
p - predicted probability observation $o$ is of class $c$

实验中所用代码

模型：

import torch

# Prepare dataset
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])

# Design model using Class
class LogisticRegressionModel(torch.nn.Module):
  def __init__(self):
    super(LogisticRegressionModel, self).__init__()
    self.linear = torch.nn.Linear(1, 1)
  def forward(self, x):
    y_pred = torch.sigmoid(self.linear(x))
    return y_pred
  
model = LogisticRegressionModel()

# Construct loss and optimizer
criterion = torch.nn.BCELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

# Training cycle
for epoch in range(1000):
  y_pred = model(x_data)
  loss = criterion(y_pred, y_data)
  print(epoch, loss.item())

  optimizer.zero_grad()
  loss.backward()
  optimizer.step()

图形化：

  import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 10, 200)
x_t = torch.Tensor(x).view((200, 1))  # 类似于numpy中的reshape
y_t = model(x_t)
y = y_t.data.numpy()
plt.plot(x, y)
plt.plot([0, 10], [0.5, 0.5], c='r')
plt.xlabel('Hours')
plt.ylabel('Probability of Pass')
plt.grid()
plt.show()

在Colab上运行

课程来源：《PyTorch深度学习实践》完结合集

mhlwsk的博客

《PyTorch深度学习实践》6.逻辑斯蒂回归笔记

逻辑斯蒂回归

分类问题

逻辑函数

实验中所用代码