Andrew Ng序列模型 笔记

发表于 | 更新于 | | 阅读次数：

Andrew Ng循环序列模型 学习笔记

笔记课程来源：https://mooc.study.163.com/learn/2001280005

应用例子

  1. 语音识别
  2. 音乐生成
  3. 情感分类
  4. DNA序列分析
  5. 机器翻译
  6. 视频活动识别
  7. 命名实体识别

image-20200802184812691

数学符号

Notation

对于每个例子，采用$x^{<i>}$来表示例子的第$i$个单词，采用$y^{<i>}$来表示第$i$个单词的标签，具体如下：

x Harry Potter and Hermione Graner invented a new spell
Element $x^{<1>}$ $x^{<2>}$ $x^{<3>}$ $x^{<4>}$ $x^{<5>}$ $x^{<6>}$ $x^{<7>}$ $x^{<8>}$ $x^{<9>}$
y 1 1 0 1 1 0 0 0 0
Label $y^{<1>}$ $y^{<2>}$ $y^{<3>}$ $y^{<4>}$ $y^{<5>}$ $y^{<6>}$ $y^{<7>}$ $y^{<8>}$ $y^{<9>}$

采用$T_x$和$T_y$表示输入序列的元素数和输出序列的元素数，如上例中$T_x=9, T_y=9$。在上例中$T_x=T_y$，但要注意在有的序列模型中这是不成立的

对于不同实例的表示，用$x^{(i)}$（注意这里是圆括号，上面采用的是尖括号）表示第$i$个例子，这样对于第$i$个实例，输入的第$t$个元素表示为$x^{(i)<t>}$，输出（标签）的第$t$个元素表示为$y^{(i)<t>}$；输入的元素数为$T_x^{(i)}$，输出的元素数为$T_y^{(i)}$

Representation

Andrew Ng在这里采用了one-hot方法进行讲解

词典与单词

词典为一个$n$维向量空间，每一维表示一个单词
单词为一个$n$为向量，每个单词由$n-1$维的$0$和$1$维的$1$表示，这个$1$代表词典中对应位置的单词

词典有大小限制，通常在几万之间，词典中词的选择有很多方法，其中包括选择高频词（当然要去掉停用词）

实际问题中可能出现不在词典中的词，一种做法是采用一个特殊的标记（token）来表示这类单词（如UNK, Unknown Word）

循环神经网络

一种简单的思路

对于序列问题，一种Naive的做法是直接采用一个标准的神经网络：

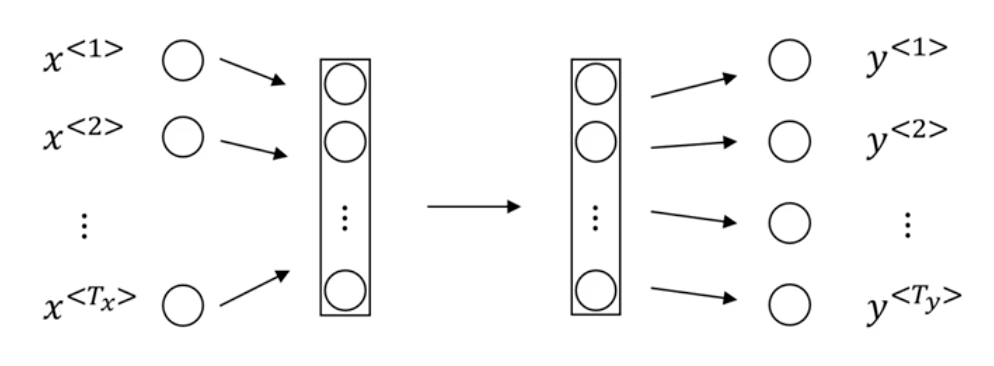
image-20200802193236668

但这个模型有两个主要问题：

  1. 输入输出在不同的例子中有不同的长度 就算是每个句子有最长长度，采用了pad或zero pad方法进行填充，也仍不是好的表示方法
  2. 句子中的不同位置不能共享学到的特征（Don’t share features learned across different positions of text） 这会导致巨大的参数量（类似于全连接神经网络对比CNN，后者的一大特点是可以共享特征，减小了参数量，同时有助于泛化，比如在图片中一个学到的物体换一个位置还能识别出来）

循环神经网络（Recurrent Neural Network）

基本概念

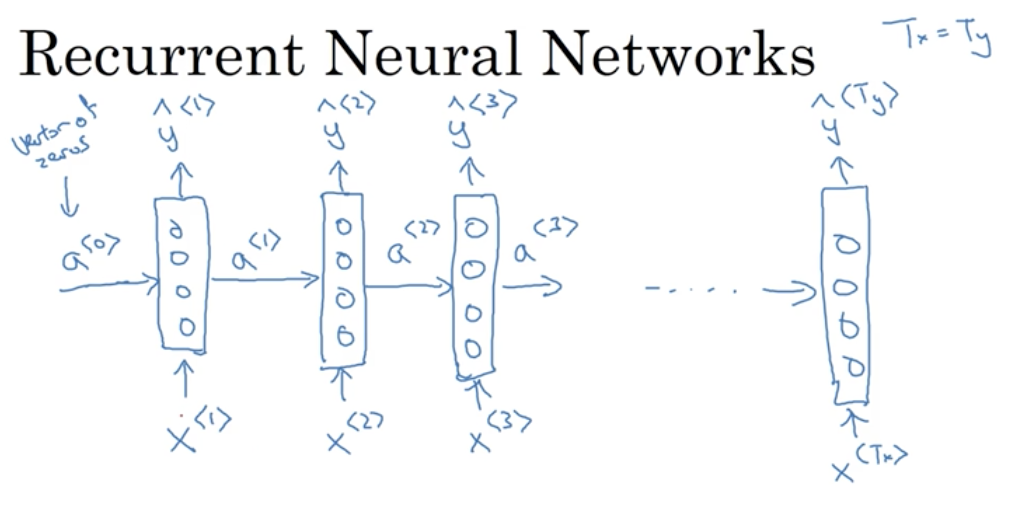
image-20200802194724987

循环神经网络是分状态共享参数的，如上图是展开的循环神经网络，每个矩形代表不同时刻下的模型，模型从左向右扫描，每个状态读入一个符号输入$x^{<i>}$和从上个状态传来的激活值$a^{<i>}$，输出这个状态的预测值$\hat{y}^{<1>}$，并传递一个激活值$a^{<i+1>}$给下一个状态

对于循环网络的开头$a^{<0>}$，需要自行选择一个值作为零时刻的伪激活值，如随机值或0

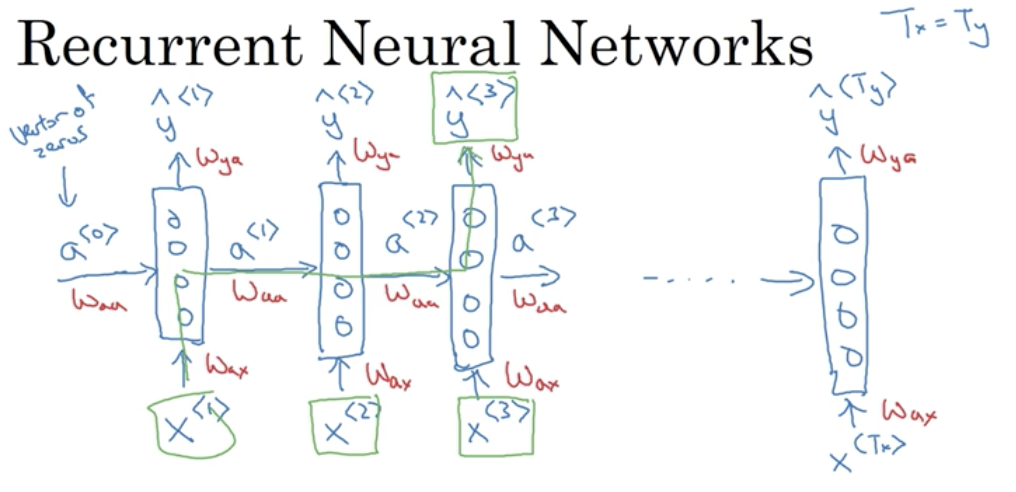
image-20200802195415641

RNN中有几套参数，输入端的$W_{ax}$，激活端的$W_{aa}$和输出端的$W_{ya}$。每个状态$i$不仅仅用到它前一个状态$i-1$的信息，还能用到它之前所有状态$i-1, i-2, \dots$的信息，这是因为信息是沿着激活值$\dots, a^{<i-2>},a^{<i-1>}$一路传过来的。但状态$i$不能用到它之后的状态$i+1, i+2, \dots$的信息，而这些信息有时候是很有用的，比如：

He said, “Teddy Roosevelt was a great President”

在对Teddy Roosevelt做人名识别时，”was a great President”是能帮助判断的，而仅通过”He said”则很难判断Teddy是人名的一部分，如下面的例子：

He said, “Teddy bear are on sale”

不能采用双向输入的问题可以采用双向循环神经网络（BRNN）来解决，在之后会提及

Forward Propagation

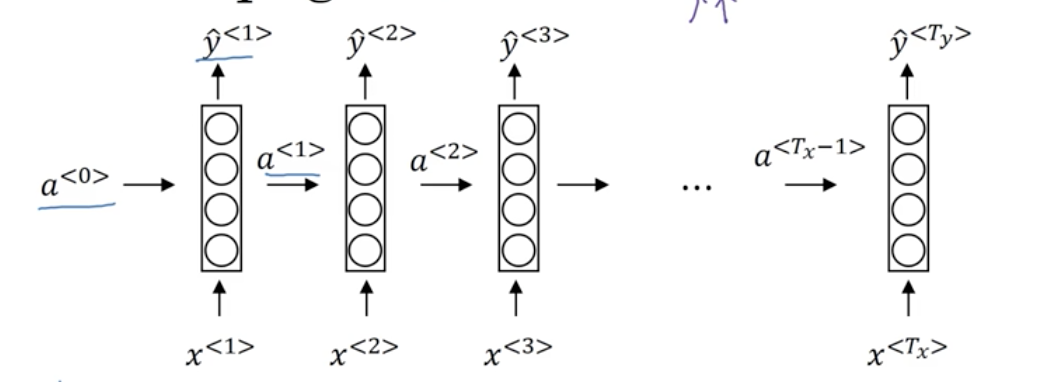
image-20200802201033326

初始化零时刻的伪激活值为零向量$a^{<0>}=\vec{0}$
接下来对于下个状态的$a$和$y$有：
$a^{<1>}=g(W_{aa}a^{<0>}+W_{ax}x^{<1>}+b_a) \leftarrow \text{这里的激活函数}g\text{经常选择}tanh\text{或}ReLU\text{，相对来说}tanh\text{更常见些}$

$\hat{y}^{<1>}=g_2(W_{ya}a^{<1>}+b_y) \leftarrow \text{如果是二分类问题，那么激活函数}g\text{一般用}sigmoid\text{，如果是k分类问题，则可以用}softmax$

更通用的写法：

$a^{<t>}=g(W_{aa}a^{<t-1>}+W_{ax}x^{<t>}+b_a)$ $\hat{y}^{<t>}=g_2(W_{ya}a^{<t>}+b_y)$

刚看到这里的时候我有个问题：$\hat{y}^{<t>}$没有利用当前的输入$x^{<t>}$的信息，而是只采用了之前状态传来的$a^{<t>}$的信息，那么是不是第一个状态$\hat{y}^{<1>}$的输出是与输入无关的？

这个问题是不存在的，因为计算$\hat{y}^{<t>}$所用到的$a^{<t>}$就是当前轮迭代中由第一个公式算出来的，而这个公式用到了输入$x^{<t>}$

简化的公式

这里简化示例直接引用用Andrew Ng的slide：

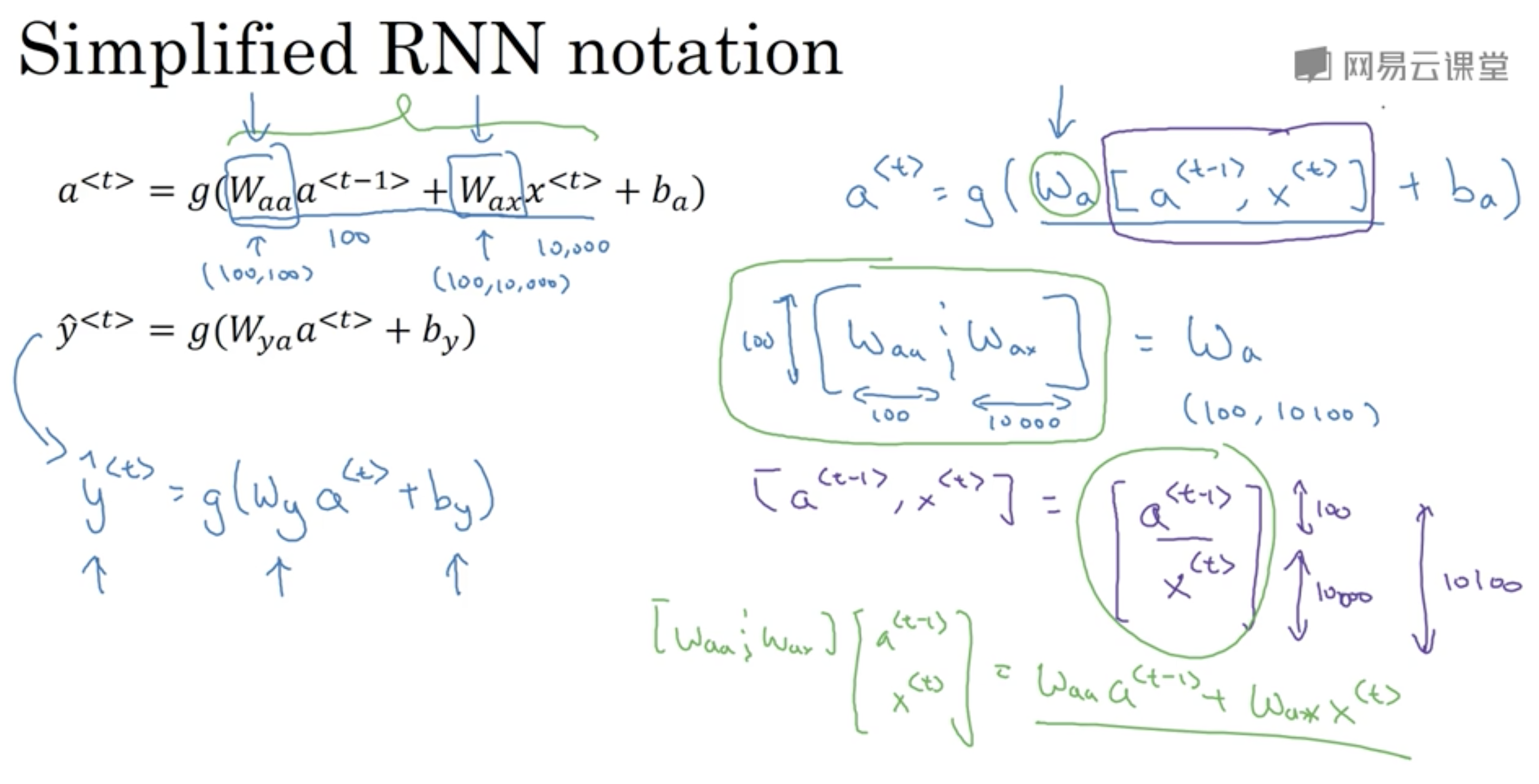
image-20200802204918980

$W_{aa}$和$W_{ax}$被合并为$W_x$，$W_{ya}$被简化为$W_y$，$a^{t-1}$和$x^{t}$被vstack（垂直拼接）为一个向量。具体合并方法见图示

这样公式简化为：

$a^{<t>}=g(W_a[a^{<t-1>},x^{<t>}]+b_a)$ $\hat{y}^{<t>}=g_2(W_{y}a^{<t>}+b_y)$

其中$W_a[a^{<t-1>},x^{<t>}]$对应：
$$W_a[a^{<t-1>},x^{<t>}]= \left[ \begin{matrix} \begin{array}{c:c} W_{aa} & W_{ax} \end{array} \end{matrix} \right] \left[ \begin{matrix} a^{<t-1>} \\ x^{<t>} \end{matrix} \right] =W_{aa}a^{t-1}+W_{ax}x^{<t>}$$

通过时间的反向传播

损失函数

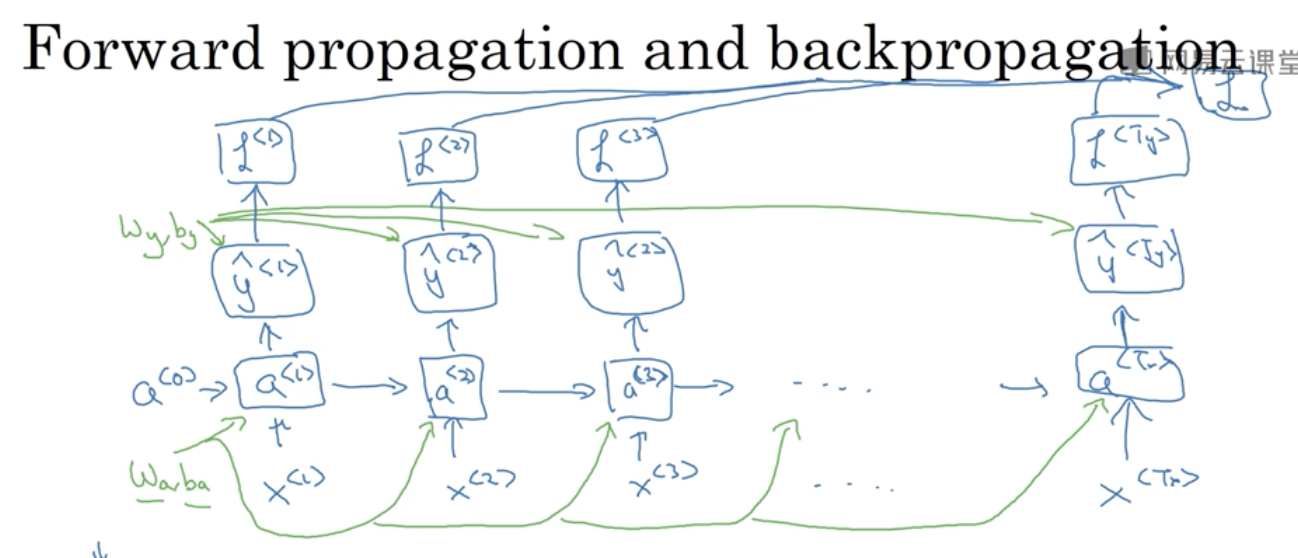
image-20200802212042028

$\mathcal{L}^{<t>}(\hat{y}^{<t>},y^{<t>})=-y^{<t>}\log\hat{y}^{<t>}-(1-y^{<t>})\log(1-\hat{y}^{<t>})$ $\mathcal{L}(\hat{y},y)=\sum^{T_y}_{t=1}\mathcal{L}^{<t>}(\hat{y}^{<t>},y^{<t>})$

每个状态的损失函数是一个交叉熵，这个RNN的损失函数是每个状态损失的和

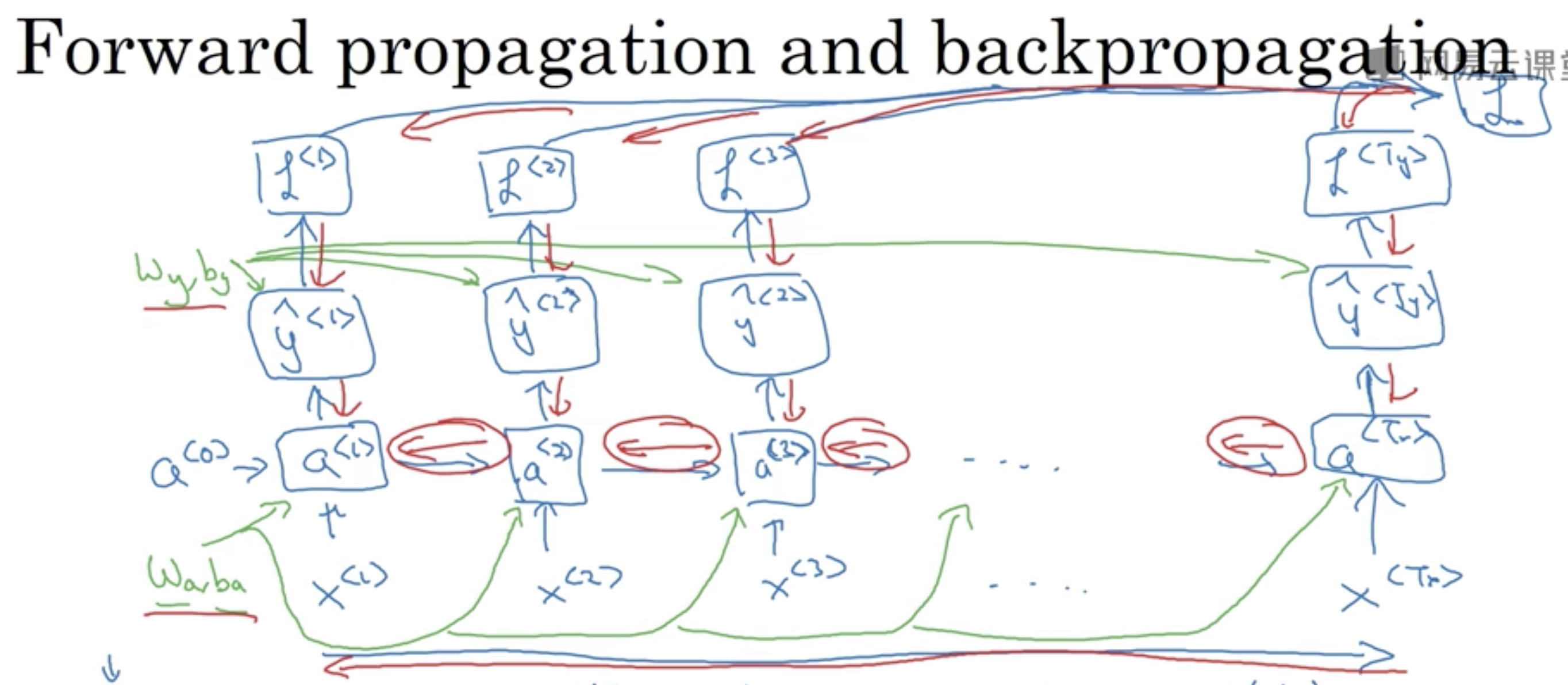
image-20200802213135277

用反向的随机梯度下降法来更新参数，其中有一个信息的反向传递尤为重要，就是上面红圈标注的，这个反向传播算法有一个专门的名字backpropagation through time

不同类型的神经网络

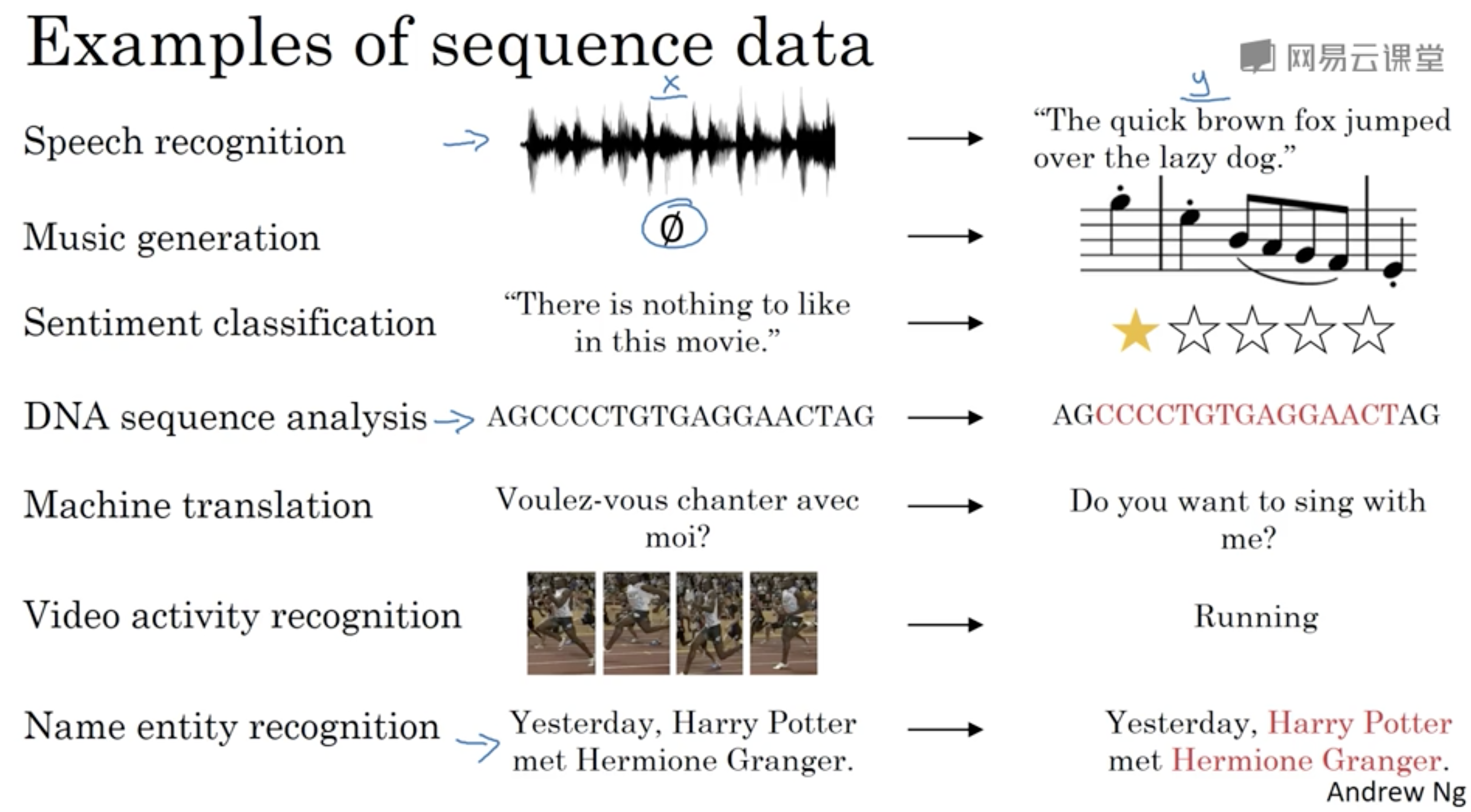
image-20200802184812691

不用的序列模型输入和输出差异是很大的，其中不一定有$T_x=T_y$，比如音乐生成的输入为空集，情感分类的输入为序列而输出为一个分类等，机器翻译的输入语言和输出语言长度不一定相等

分类

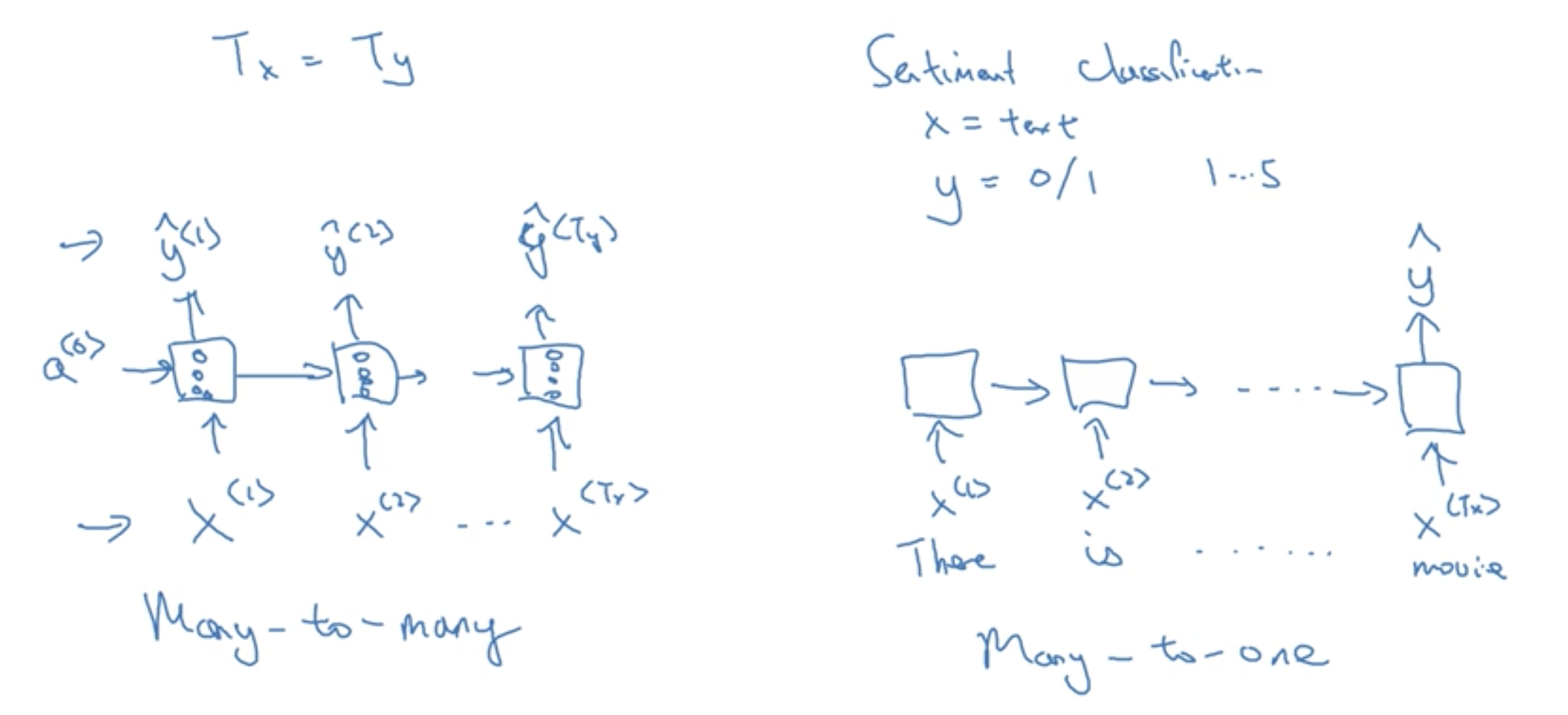
image-20200802214524237

左图的RNN为常规的RNN，每个状态都有一个输入和输出，是Many-to-many的，右图的RNN为只有一个输出（这里的例子是针对情感分类任务），是Many-to-one的。当然其实还有One-to-one的，这种神经网络只有一个时间状态，就是传统意义上的神经网络

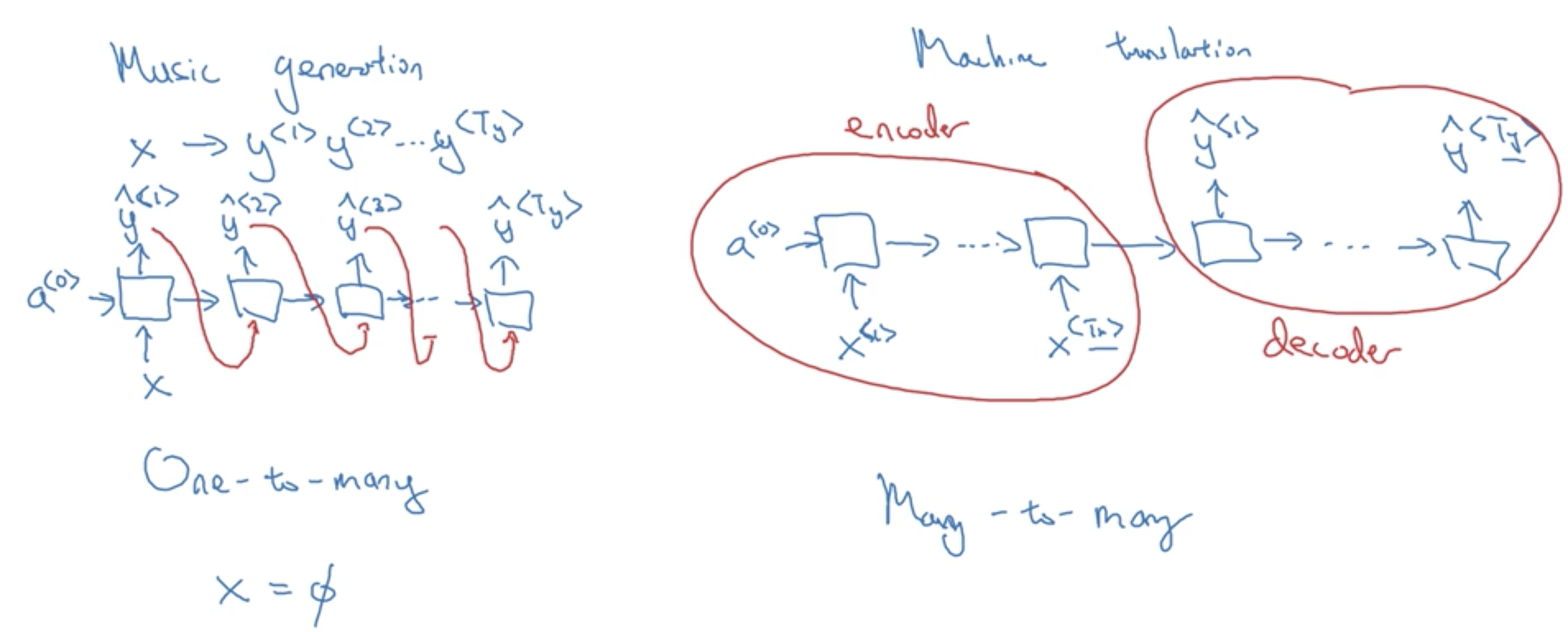
image-20200802215430664

上图中的左图为一个用于音乐生成的RNN，这是一个One-to-many的RNN，它的第一个输入为音乐的第一个音符♪或者音乐的类型，或者零向量（即表示空集），其后便只有输出没有输入

上图中的右图为一个用于机器翻译的RNN，它是一个Many-to-many的RNN，这个RNN先连续读入一段输入，再连续输出结果。这个RNN的前一段称为encoder，后一段称为decoder

语言模型和序列生成

基本任务

判断一个序列的先验概率

The apple and pair salad
The apple and pear salad

$$P(\text{The apple and pair salad})=? \\ P(\text{The apple and pear salad})=?$$

Tokenization

获得每个单词（含\, UNK等）的token化表示

Cats average 15 hours of sleep a day. \

这里直接采用了上面提到的one-hot进行表示，$n$维向量，其中1维为1，其它维为0，表示对应位置的单词

模型

模型的结构为一个Many-to-many的RNN

与基于统计的语言模型直接基于语料库计算后验概率不同，基于RNN的语言模型把语料库的每条语句的单词序列作为输入，预测的下个单词的序列作为输出来训练模型：

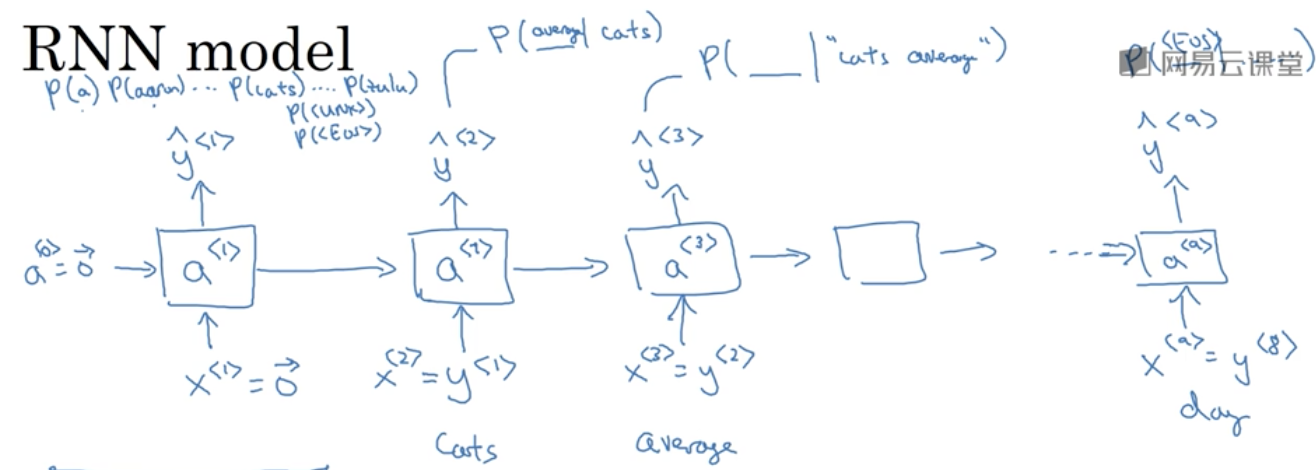
image-20200809203355448

$a^{<0>}$和$x^{<1>}$作为初始输入都为零向量，后面的$\hat{y}^{<i>}$和$x^{<i+1>}$是对应的，即$x^{<i+1>}$不仅仅是$i+1$状态的输入，还是$i$状态输出的实际值（或者说label）。$i$状态的输出为一个$n$维向量，第$i$维表示$P(y^{<i>}=W_i|y^{<i-1>}y^{<i-2>}\cdots)$，其中$W_i$表示one-hot向量中第$i$个位置对应的词表中第的$i$单词。$i$状态的输出是通过softmax函数得出的，一方面代表输出出每个单词的概率，另一方面最大概率的那个下标也是预测的单词。这个RNN的loss函数可以计算状态输出和实际值的交叉熵，形式与前面的交叉熵类似：

$\mathcal{L}(\hat{y}^{<t>},y^{<t>})=-\sum_i{y_i^{<t>}\log\hat{y}_i^{<t>}}$ $\mathcal{L}=\sum_t\mathcal{L}^{<t>}(\hat{y}^{<t>},y^{<t>})$

如果要计算一个句子的概率，如上文中的Cats average 15，则代入公式$P(y^{<1>},y^{<2>},y^{<3>})=P(y^{<1>})P(y^{<2>}|y^{<1>})P(y^{<3>}|y^{<1>}y^{<2>})$

其中$P(y^{<1>}), P(y^{<2>}|y^{<1>})$和$P(y^{<3>}|y^{<1>}y^{<2>})$可分别由$1,2$和$3$状态的输出获得

对新序列采样

要检验模型确实学到了东西，可以尝试对序列进行采样

词语级别的语言模型（Word-level language model）

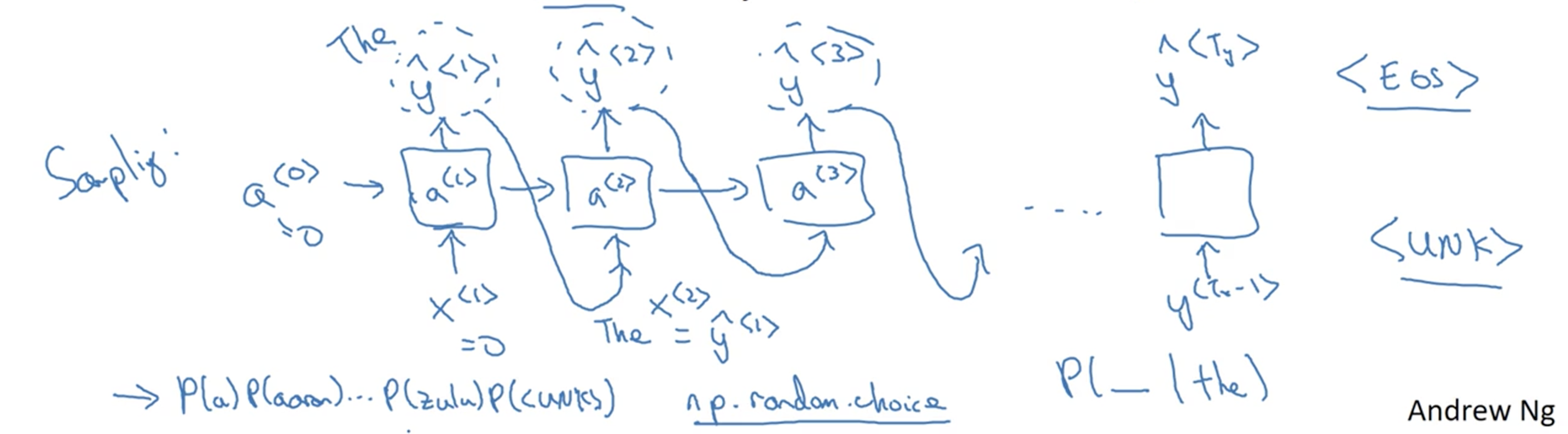
image-20200930165919635

从$x^{<1>}$开始指定一个输入。接下来从它算出的输出$\hat{y}^{<1>}$（注：$\hat{y}^{<1>}$是一个概率分布矩阵）中随机选择（准确地说是根据概率分布选择）一个label作为下一个状态的输入$x^{<2>}$。对于后面的输出和输入按照这样的方法进行操作，输出的label就可以构成一个句子。如何停止：一种方法是生成了<EOS>标记；另一种是可以指定生成的长度，如20。

为什么要根据概率分布选择而不是直接用argmax：如果直接用argmax，相同的初始输入$x^{<1>}$得到的句子输出是完全一样的。

另外，要避免生成<UNK>这种未知单词。

字符级别的语言模型（Character-level language model）

优点：主要是不存在词典中未登录词的问题，对于每一个单词都能给出一个概率分布，同时词表会很小

缺点：生成的序列很长，难以解决长距离依赖问题，而且训练成本比较高

带有神经网络的梯度消失问题

句子中可能出现长距离依赖问题，如：

The cat, which already ate ….. , was full

The cats, which already ate ……, were full

全连接神经网络存在梯度消失问题。在非常深的网络中，权重更新会变得很困难。具体地，在反向传播过程中，从输出$\hat{y}$得到的梯度很难传播回去影响到前面层的权重。

image-20201015143544087

RNN网络具有相似的问题，更具体地，是无法解决句子中的长距离依赖问题。

深度神经网络中还可能出现梯度爆炸的问题，在实践中一般模型训练会直接失败，参数中会出现许多的NaN。一个解决方法是采用梯度修剪（gradient clipping），如果梯度梯度向量大于某个阈值，缩放整个梯度向量。梯度爆炸比梯度消失更容易解决。

GRU门控循环单元

回顾RNN

RNN的基本公式包括一个激活值$a$和预测值$\hat{y}$的计算：
$a^{<t>}=g(W_a[a^{<t-1>},x^{<t>}]+b_a)$

$\hat{y}^{<t>}=g_2(W_{y}a^{<t>}+b_y)$

RNN单元进行可视化，可以表示为下图：

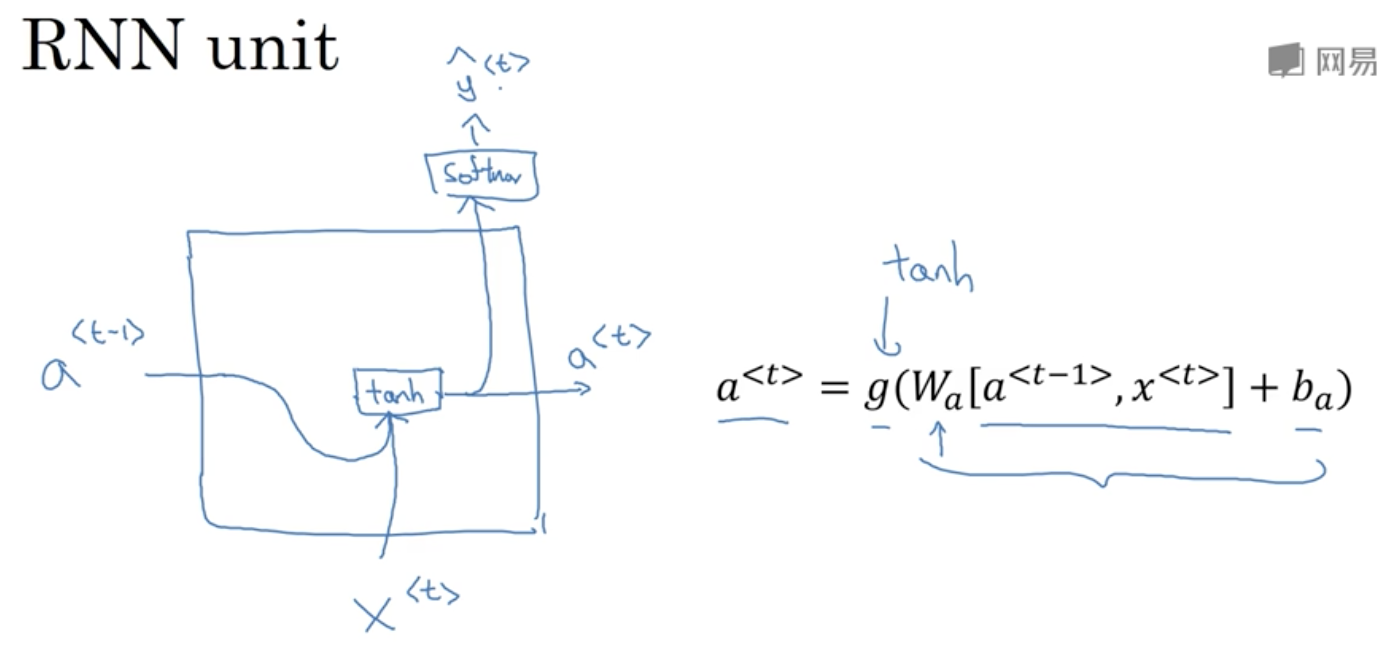
image-20201015150430055

简化的GRU单元结构

首先理解一个简化版的GRU，与RNN相比，它在计算激活值$a$上添加对长距离依赖的支持。

记$c$为记忆单元（memory cell），用于存储当前的记忆信息。在GRU中，有$c^{<t>}=a^{<t>}$，其中$a^{<t>}$对应RNN中上一个状态传来的激活值。

这个简化版GRU的基本公式如下（这里去掉了与RNN相同的计算$\hat{y}$的部分）：
$\tilde{c}^{<t>}=\tanh(\omega_c[c^{<t-1>},x^{<t>}]+b_c)$

$\Gamma_u=\sigma(\omega_u[c^{<t-1>},x^{<t>}]+b_u)$ $c^{<t>}=\Gamma_u*\tilde{c}^{<t>}+(1-\Gamma_u)*c^{<t-1>}$

可以看出来计算$\tilde{c}^{<t>}$和$\Gamma_u$的公式与RNN中更新$a$的公式$a^{<t>}=g(W_a[a^{<t-1>},x^{<t>}]+b_a)$非常相似，都是激活值$a$（在GRU中为记忆单元$c$）与输入$x$一起乘以一个参数矩阵$W$（GRU中为$\omega$），加上一个偏置矩阵$b$，最后再经过一个激活函数。不同的是GRU多了一个更新门$\Gamma_u$的计算用于控制遗忘，同时对记忆单元$c$（注意没有波浪线上标）的更新更为复杂。

其中$\tilde{c}^{<t>}$是$c^{<t>}$的候选值，用于更新$c^{<t>}$的值；而$\Gamma_u$为一个更新门（Update Gate），是一个(0,1)的矩阵，用于决定是否用当前的$\tilde{c}^{<t>}$来更新$c^{<t>}$（或者说遗忘之前的信息）；最后计算$c^{<t>}$，对记忆单元$c$执行实际的更新操作（即是否用当前的信息$\tilde{c}^{<t>}$替换掉之前的记忆$c^{<t>}$）。

其中$\Gamma_u$的激活函数是Sigmoid，为方便理解这里可以认为$\Gamma_u$的取值为0或1，即用于控制$c^{<t>}$是否更新（遗忘）。$\Gamma_u*\tilde{c}^{<t>}$为数乘，若$\Gamma_u$为1，则表示用当前的候选值$\tilde{c}^{<t>}$来更新$c^{<t>}$（同时遗忘之前的记忆）；为0则表示不更新，以此保存之前的记忆。

另外需要注意的是$\Gamma_u$、$\tilde{c}^{<t>}$和$c^{<t>}$可以是多维的。这种情况下，$\Gamma_u$某一维的01取值决定了$c^{<t>}$的对应维是否更新。

简化版GRU相比于RNN的改进主要是引入了一个更新门$\Gamma_u$，它使得某些$c$某些维的信息可以维持很多轮不更新，这样就保持了之前的记忆，解决长距离依赖问题。

这个简化版的GPU进行可视化，可以表示为下图，可以看出，这个简化版的GRU和RNN在输入输出的形式上是一样的，但$c$的计算引入了遗忘机制。

image-20201015165916497

完整的GRU单元结构

完整的GRU结构与上面简化的版本相比，基本思想是相同的，不同之处在于计算$\tilde{c}$时引入了一个新的相关门$\Gamma_r$。至于为什么这么用，诶Andrew给出的解释是实验得出的。
$\tilde{c}^{<t>}=\tanh(\omega_c[\Gamma_r*c^{<t-1>},x^{<t>}]+b_c)$

$\Gamma_u=\sigma(\omega_u[c^{<t-1>},x^{<t>}]+b_u)$ $\Gamma_r=\sigma(\omega_r[c^{<t-1>},x^{<t>}]+b_r)$ $c^{<t>}=\Gamma_u*\tilde{c}^{<t>}+(1-\Gamma_u)*c^{<t-1>}$

LSTM单元结构

相比于GRU，LSTM单元的结构要更加复杂，但也更强大。

与GRU不同，LSTM中，$c^{<t>}\neq a^{<t>}$，$c$与$a$是分别计算的；不再采用相关门$\Gamma_r$；$c^{<t>}$的更新不只由更新门$\Gamma_u$控制，而是由更新门$\Gamma_u$和一个新的遗忘门$\Gamma_f$控制；$a^{<t>}$的更新由一个额外的输出门$\Gamma_o$控制
$\tilde{c}^{<t>}=\tanh(\omega_c[c^{<t-1>},x^{<t>}]+b_c)$

$\Gamma_u=\sigma(\omega_u[a^{<t-1>},x^{<t>}]+b_u)$ $\Gamma_f=\sigma(\omega_f[a^{<t-1>},x^{<t>}]+b_f)$ $\Gamma_o=\sigma(\omega_o[a^{<t-1>},x^{<t>}]+b_o)$ $c^{<t>}=\Gamma_u*\tilde{c}^{<t>}+\Gamma_f*c^{<t-1>}$ $a^{<t>}=\Gamma_o*c^{<t>}$

LSTM单元进行可视化，可以表示为下图：

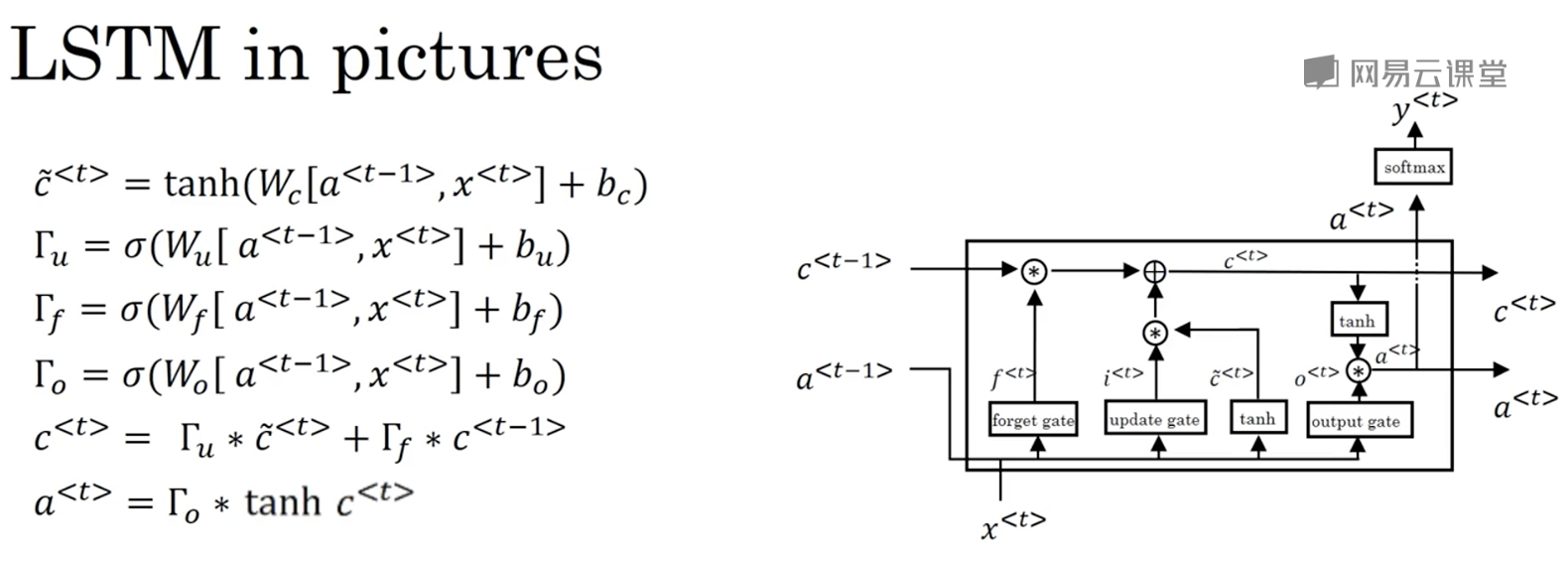
image-20201016171732787

LSTM有3个门而GRU有2个门。与GRU相比，LSTM的单个单元要更加强大和灵活，但计算代价要更大；GRU适合构造更大规模的网络。

双向神经网络

单向神经网络只能利用一个方向的语义信息，但有时这是不够的。

He said, “Teddy bears are on sale!”

He said, “Teddy Roosevelt was a great President!”

比如上面的例子，要判断Teddy是人名还是泰迪熊，需要用到句子后面的信息。

双向RNN的结构如下图，激活函数需要用到来自两个方向的激活值：

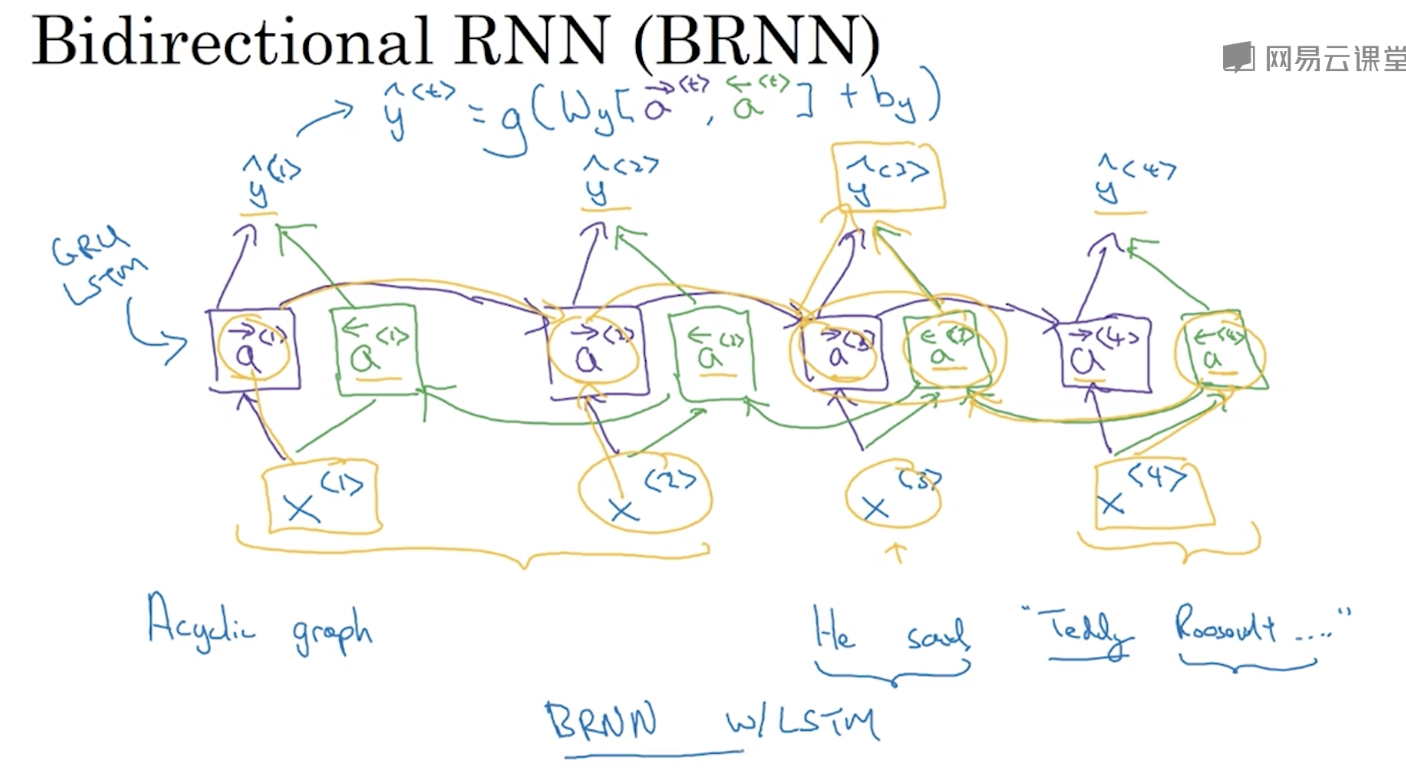
image-20201016210337843

其中的单元不仅可以是普通的RNN单元，还可以是GRU或LSTM单元，对应BiGRU或BiLSTM。

双向神经网络的缺点：双向神经网络要求获取完整的序列数据，这在语音识别等场景下不是非常适用（如语音识别需要说话者说完一整句话才能开始识别）。

深层循环神经网络

RNN可以在结构上嵌套以构造深层的网络结构。深层RNN的结构分为两个维度，分别是横向的时间维度和纵向的维度。每一个单元可以利用到之前时间和之前层的激活值。而横向时间维度和纵向的维度是相互独立的，即可以出现在前两个时刻疯狂堆层数来预测$y^{<1>}$和$y^{<2>}$，而这些层在横向上并不相连的情况。

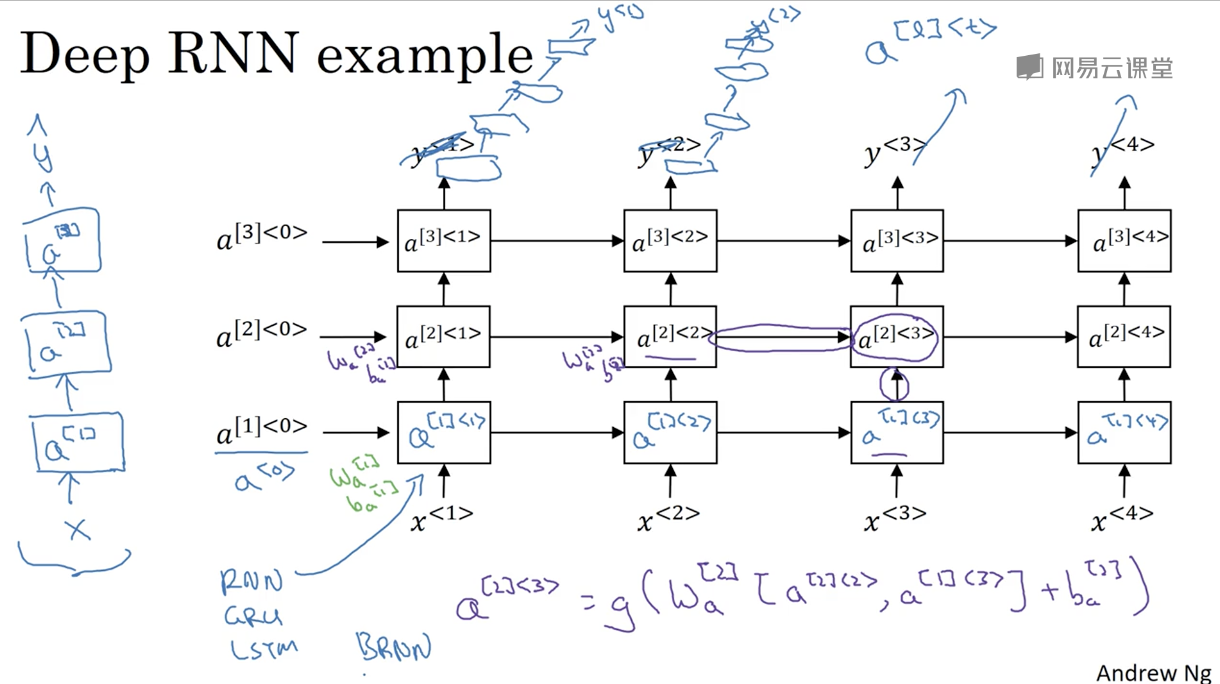
image-20201016211416102

由于深层RNN多了一个横向的时间维度，有少量的层数RNN网络其实已经非常大了。所以与深层CNN相比，深层RNN在深度上会浅一些。