《PyTorch深度学习实践》3.梯度下降算法

梯度下降算法

减小loss的暴力算法

直接枚举，时间复杂度过高

分段枚举（如下图），先大粒度枚举（图中16个红色的点），再挑选较优点小粒度枚举（用绿色网格表示），可以减小枚举次数（如图中从直接枚举的256次减小到16+16=32次）。但分段枚举也有问题，无法解决局部最优和导数为0的点

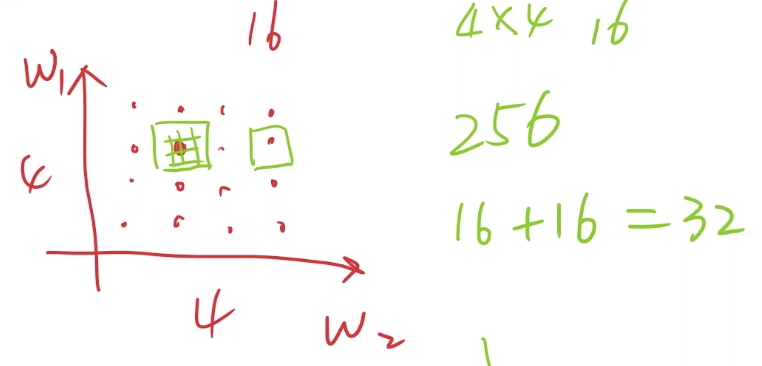
梯度下降算法

基本思想

梯度公式：
$gradient=\frac{\partial{cost}}{\partial{\omega}}$

参数更新：

$\omega = \omega - \alpha \frac{\partial{cost}}{\partial{\omega}}$

优化方向为梯度上升方向的反方向

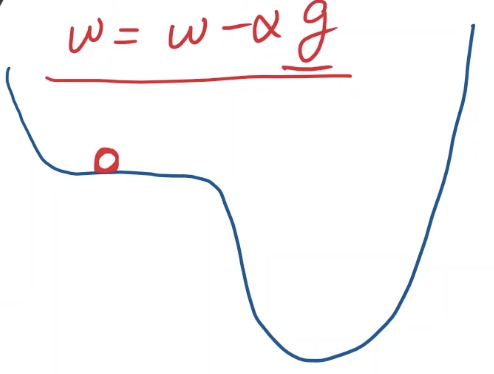
梯度下降算法也避免不了局部最优

另一种特殊的情况为鞍点（saddle point），这种点梯度为0，一旦到达这个位置，梯度下降就无法继续进行了

公式在线性模型MSE的应用

梯度计算：

$$\begin{align} \frac{\partial{cost(\omega)}}{\partial{\omega}}&=\frac{\partial}{\partial{\omega}}\frac{1}{N}\sum_{n=1}^{N}(x_n\omega - y_n)^2 \\ &=\frac{1}{N}\sum_{n=1}^{N}\frac{\partial}{\partial{\omega}}(x_n\omega - y_n)^2 \\ &=\frac{1}{N}\sum_{n=1}^{N}2\cdot (x_n\omega - y_n)\frac{\partial{(x_n\omega - y_n)}}{\partial{\omega}} \\ &=\frac{1}{N}\sum_{n=1}^{N}2\cdot x_n (x_n\omega - y_n) \end{align}$$

参数更新：

$\omega = \omega -\alpha \frac{1}{N}\sum_{n=1}^{N}2\cdot x_n (x_n \cdot \omega - y_n)$

代码参考：

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w = 1.0

def forward(x):
    return x * w

def cost(xs, ys):
    cost = 0
    for x,y in zip(xs, ys):
        y_pred = forward(x)
        cost += (y_pred - y) ** 2
    return cost / len(xs)

def  gradient(xs, ys):
    grad = 0
    for x, y in zip(xs, ys):
        grad += 2 * x * (x * w - y)
    return grad / len(xs)

print('Predict (before training', 4, forward(4))
for epoch in range(100):
    cost_val = cost(x_data, y_data)
    grad_val = gradient(x_data,  y_data)
    w -= 0.01 * grad_val
    print('Epoch:', epoch, 'w=', 'loss=', cost_val)
print('Predict (after training', 4, forward(4))

正常情况下，loss应该是单调递减的（中途可能出现波动），最终应该是收敛的，如果不收敛，说明函数本身不收敛，或者更常见的情况是学习率取大了

随机梯度下降SGD

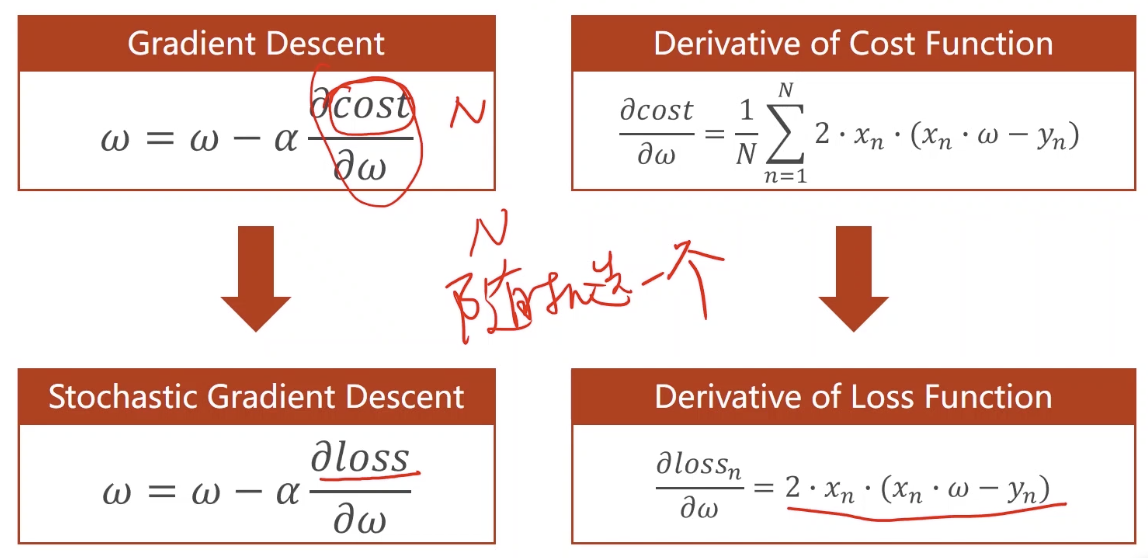
这里讲到的SGD相对于上面的梯度下降的不同是每次更新只考虑一个样本而不是所有样本。相比于神经网络中一次更新一个batch的做法是一个简化版

代码参考：

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w = 1.0

def forward(x):
    return x * w

def loss(xs, ys):
    y_pred = forward(x)
    return (y_pred - y) ** 2

def  gradient(xs, ys):
    return 2 * x * (x * w - y)

print('Predict (before training', 4, forward(4))
for epoch in range(100):
    for x, y in zip(x_data, y_data):
        grad = gradient(x, y)
        w = w - 0.01 * grad
        print("\tgrad: ", x, y, grad)
        l = loss(x, y)
    print("progress:", epoch, "w=", w, "loss=", 1)

print("Predict (after training)", 4, forward(4))

在Colab上运行

课程来源：《PyTorch深度学习实践》完结合集