《PyTorch深度学习实践》9. 多分类问题

发表于 | | 阅读次数：

多分类问题

N分类问题（N>2）最朴素的解决方案是拆分为N个二分类问题。但这样做的问题是不同类别间应该是互斥的（或者说相互抑制），直接拆分的话可能每个类别的概率都很高（或者加起来不等于1）。

Softmax Layer

假定$z^l\in\mathbb{R}^K$ 是最后一个线性层的输出，softmax layer的形式为：

$P(y=i)=\frac{e^{z_i}}{\sum_{j=0}^{K-1}e^{z_j}},i\in\{0,\dots,K-1\}$

Softmax layer的好处是可以把最后一层的输出归一化为每一类[0,1]的概率，且概率和为1

注：之前的朴素二分类问题，因为最后一层以sigmoid函数结尾，只有一个[0,1]的输出，本身符合概率定义，所以不需要用softmax。损失的计算直接用二类交叉熵就行了。

Softmax的损失函数

Softmax层后接的损失函数仍然可以用交叉熵， 如图（NLLLoss, negative log likelihood loss）：

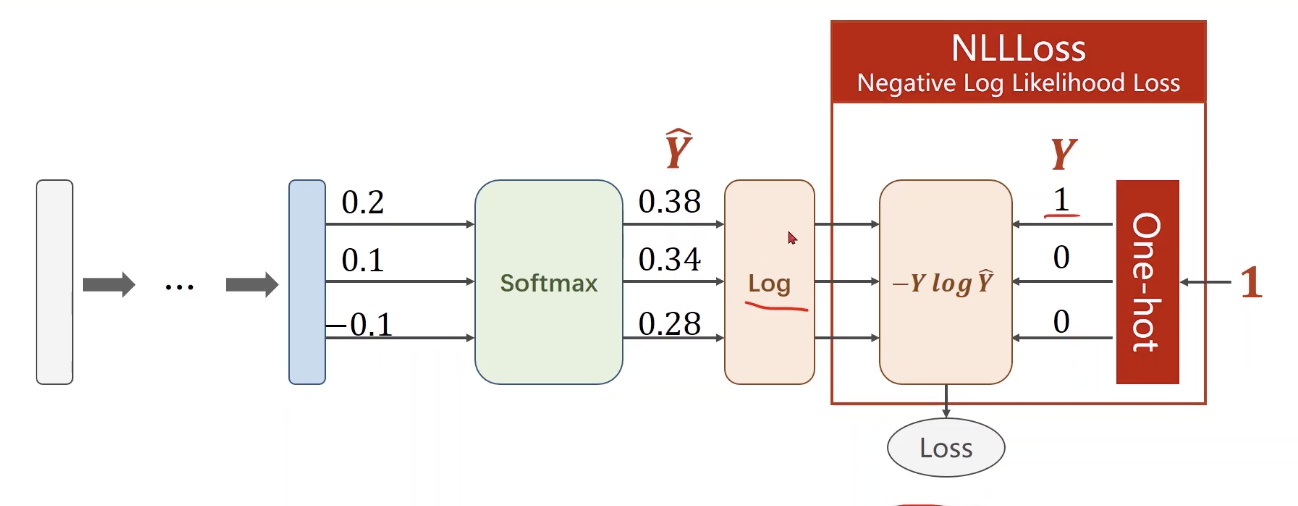
image-20200919112307060

具体公式为$Loss(\hat{Y},Y)=-Y\log\hat{Y}$，上图中最右侧的1为label，经过一个binarizer转化为one-hot表示，即一个维数为label类别总数的01向量，其中只有一维为1。这个向量作为$Y$，与softmax层的预测值$\hat{Y}$求交叉熵。

补充一下这里采用的交叉熵公式：

$-\sum_{c=1}^My_{o,c}\log(p_{o,c})$
  • M - number of classes (dog, cat, fish)
  • log - the natural log
  • y - binary indicator (0 or 1) if class label $c$ is the correct classification for observation $o$
  • p - predicted probability observation $o$ is of class $c$

所以这里的交叉熵结果其实就是正确的那个类别预测概率（正确类别的softmax输出值）取log的负值，其它类别的概率都乘了0。

实现的基本原理：

1
2
3
4
5
6
import numpy as np
y = np.array([1, 0, 0])
z = np.array([0.2, 0.1, -0.1])
y_pred = np.exp(z) / np.exp(z).sum()
loss = (-y * np.log(y_pred)).sum()
print(loss)

采用torch中提供的CrossEntropyLoss的实现方式：

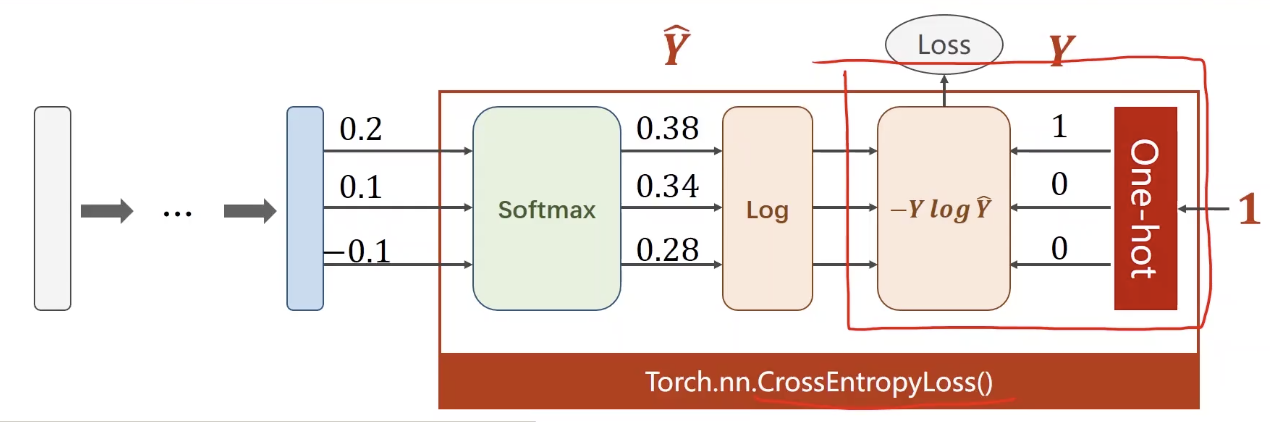
image-20200919160853359

1
2
3
4
5
6
import torch
y = torch.LongTensor([0])
z = torch.Tensor([[0.2, 0.1, -0.1]])
criterion = torch.nn.CrossEntropyLoss()
loss = criterion(z, y)
print(loss)

一个更具体的例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import torch
criterion = torch.nn.CrossEntropyLoss()

Y = torch.LongTensor([2, 0, 1]) # 对应3个样本的label

# 第一个模型的预测输出（Softmax）
Y_pred1 = torch.Tensor([[0.1, 0.2, 0.9], # 下标2的预测概率最大，实际label为2
                       [1.1, 0.1, 0.2], # 下标0的预测概率最大，实际label为0
                       [0.2, 2.1, 0.1]]) # 下标1的预测概率最大，实际label为1
# 另一个模型的预测输出（Softmax）
Y_pred2 = torch.Tensor([[0.8, 0.2, 0.3], # 下标0的预测概率最大，实际label为2
                        [0.2, 0.3, 0.5],   # 下标2的预测概率最大，实际label为0
                        [0.2, 0.2, 0.5]])  # 下标2的预测概率最大，实际label为1

l1 = criterion(Y_pred1, Y)
l2 = criterion(Y_pred2, Y)
# Batch Loss1 =  tensor(0.4966) 
# Batch Loss2= tensor(1.2389)
print("Batch Loss1 = ", l1.data, "\nBatch Loss2=", l2.data)

补充：PyTorch中CrossEntropyLoss和NLLLoss的关系：

CrossEntropyLoss<==>LogSoftmax+NLLLoss

实例：MNIST数据集训练

  • Prepare dataset

    Dataset and Dataloader

  • Design model using Class

    • Inherit from nn.Module

  • Construct loss and optimizer

  • Training cycle + Test

    • forward, backward, update
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F # 这里用了ReLU而非Sigmoid
import torch.optim as optim

batch_size = 64
transform = transforms.Compose([
            transforms.ToTensor(),
            transforms.Normalize((0.1307, ), (0.3081, ))
            # The parameters are mean and std respectively. 
])

train_dataset = datasets.MNIST(root='../dataset/mnist/',
                               train=True,
                               download=True,
                               transform=transform)
train_loader = DataLoader(train_dataset,
                         shuffle=True,
                         batch_size=batch_size)
test_dataset = datasets.MNIST(root="../dataset/mnist/",
                              train=False,
                              download=True,
                              transform=transform)
test_loader = DataLoader(test_dataset,
                         shuffle=False,
                         batch_size=batch_size)

class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.l1 = torch.nn.Linear(784, 512)
        self.l2 = torch.nn.Linear(512, 256)
        self.l3 = torch.nn.Linear(256, 128)
        self.l4 = torch.nn.Linear(128, 64)
        self.l5 = torch.nn.Linear(64, 10)

    def forward(self, x):
        x = x.view(-1, 784)
        x = F.relu(self.l1(x))
        x = F.relu(self.l2(x))
        x = F.relu(self.l3(x))
        x = F.relu(self.l4(x))
        return self.l5(x)  # 注意：返回的是一个线性层的输出，没有经过激活函数
   
model = Net()

criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)

def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        inputs, target = data
        optimizer.zero_grad()

        # forward + backward + update
        outputs = model(inputs)
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if batch_idx % 300 == 299:
            print("[%d, %5d] loss: %.3f" % (epoch + 1, batch_idx + 1, running_loss / 300))
            running_loss = 0.0
            
def test():
    correct = 0
    total = 0
    with torch.no_grad():   # 测试不需要求梯度
        for data in test_loader:
            images, labels = data
            outputs = model(images)
            _, predicted = torch.max(outputs.data, dim=1)   # 找最大概率的下标
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
    print("Accuracy on test set: %d %%" % (100 * correct / total))
    
if __name__ == "__main__":
    for epoch in range(10):
        train(epoch)
        test()

在Colab上运行

课程来源：《PyTorch深度学习实践》完结合集