Andrew Ng循环序列模型 学习笔记
笔记课程来源:https://mooc.study.163.com/learn/2001280005
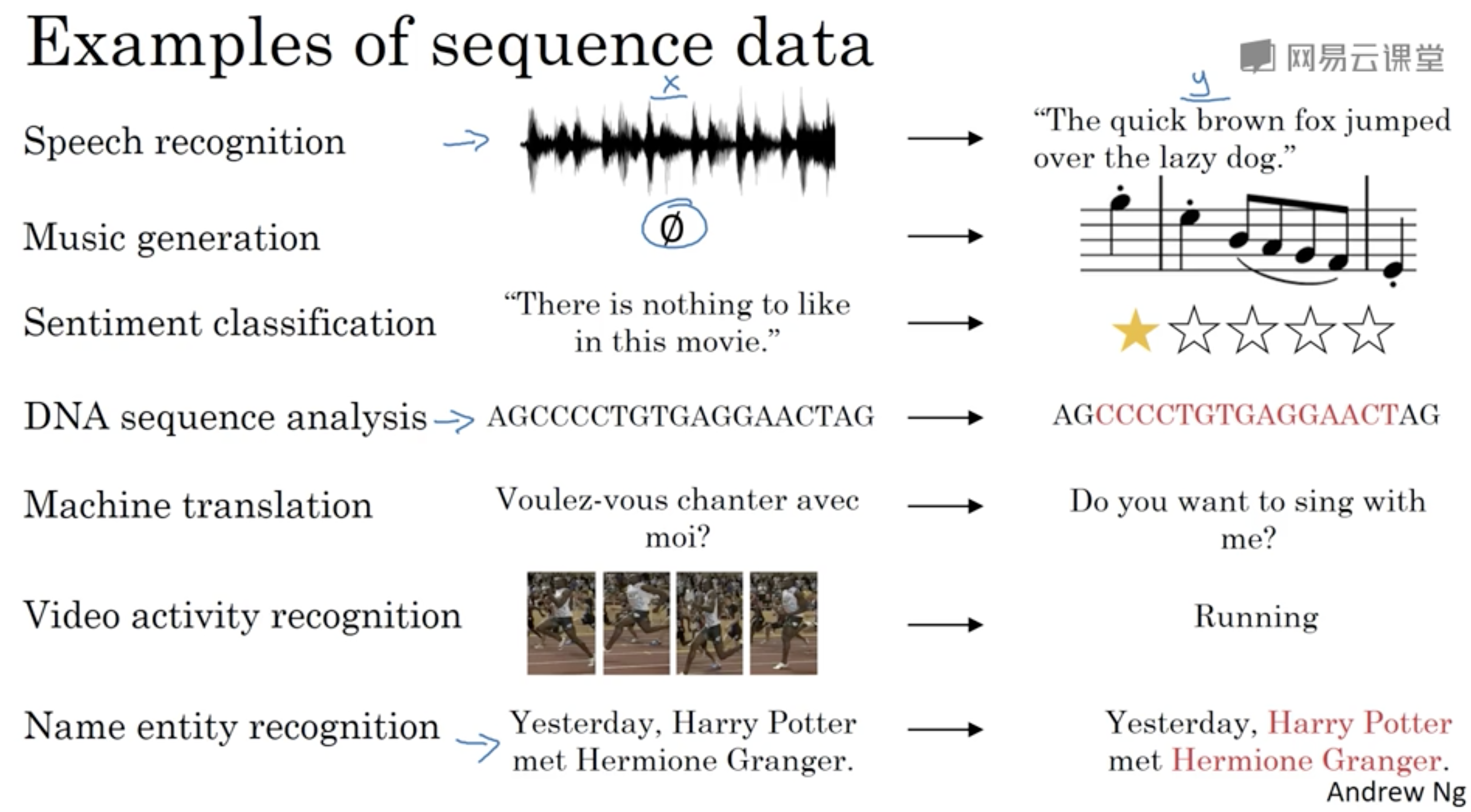
应用例子
- 语音识别
- 音乐生成
- 情感分类
- DNA序列分析
- 机器翻译
- 视频活动识别
- 命名实体识别
笔记课程来源:https://mooc.study.163.com/learn/2001280005

本文使用JGraphT存储Social Network中的人际关系图结构,使用JGraphT中的预设算法压缩建图时间。
注:这里的建图时间包含最短路求解与轨道插入,下文重点优化最短路求解时间。
之前写完软件构造Lab2时,rainywang有建议过将Lab2的Graph ADT进行封装以便之后的使用。
在写Lab3时的Social Network时,为了保存和处理关系图,一开始我直接迁移了Lab2的代码,将Lab2的ADT搬到Lab3并添加了数个API。但看到标签为Larger的几个文件,心里还是对Lab2中naïve的ADT实现感到担忧。仅仅一个返回邻接顶点的操作时间复杂度都要O(n),明显它是不能够胜任Lab3或者之后的Lab5的性能要求的。
rainywang在Lab2课程结束时,不仅建议过封装Lab2的ADT,也提出了这样一个疑问:网上是否已经有相关图算法ADT了?这个既是疑问又带有明显暗示的说法让人感到不安,显然图算法这个轮子已经被人重造过很多次了,我当然有理由相信有人已经为之写出了不错的java库。
抱着找找看的心理,在Google上尝试搜索了下”java graph library”,在返回的第一个结果发现了JGraphT,它的开源许可证为 Eclipse Public License - v 2.0。
题目链接:https://nanti.jisuanke.com/t/31445
题目大意:给定一张图,问第K最短路的长度是否小于给定值T
求第K最短路,令$f=g+h$,$g$为当前已经走过的距离,$h$为当前点到终点的最短距离
从起点开始拓展,每次选择$f$最短的点进行拓展(入队),每次出队时检查是否走到终点并统计终点出队次数,当终点出队次数为$k$时当前点的$g$就是答案
可以这样考虑:每次严格按照估价函数进行拓展,则第一次走到终点的方案一定是最短路,第二次就是第2最短路,第k次就是第k最短路
这样先用spfa预处理出每个节点的$h$再用A*拓展即可
这题还有一个需要注意的地方:A*用的优先队列很有可能在使用完后没有被清空(因为函数可能提前退出了),此时如果直接用会MLE,而如果用一个一个pop的方式清空会直接TLE,所以比较好的解决方法是直接把优先队列写在函数体内部,这样就不用清空了
题目链接:http://codeforces.com/gym/100342/attachments
题目大意:给定一张有向图,询问有多少个三元环。
这道题数据范围只有1500,所以可以n^2,我们暴力枚举两个点,假设为A->B,然后我们预处理出有哪些点可以到A,B可以到哪些点,这样就可以得到俩集合,然后再交一下,再统计一下集合里面元素的个数就好了
引用自qscqesze